* 틀린 내용이 있다면 알려주세요! 개인 공부 목적으로 전공 복습/예습을 위해 쓰는 글이라 틀린 부분이 있을 수 있습니다. 틀린 내용을 알려주시면 제게도 도움이 됩니다 :)
* 해외 대학을 재학 중이기 때문에 영어 사용이 조금 많을 수 있지만 최대한 한국어로 번역하려 노력중입니다.
* 효율적인 타이핑을 위해 "~이다" 의 문체를 사용합니다. 양해 부탁드립니다!
Introduction: 디지털 논리 회로 소개
*인트로 부분은 넘어가셔도 됩니다!
컴퓨터는 크게 메모리 유닛 (memory unit), 중앙 처리 유닛 (central processing unit), 그리고 입출력 유닛 (input and output unit) 으로 나눌 수 있다.
- 메모리 유닛: 입/출력, 프로그램, 그리고 데이터를 저장한다
- 중앙 처리 유닛: 연산, 데이터 이동을 책임진다
- 입출력 유닛: 프로그램과 데이터를 메모리 유닛으로 보내고, 출력 결과를 받는 역할을 한다
+ 여기서 흥미로운 정보: 트랜지스터는 거의 모든 논리 회로에 사용된다. 회로가 스위치처럼 역할을 수행 할 때 사용되기 때문이다(0 = off, 1 = on). 실리콘 조각(Digital integrated circuit) 위에 넣는 트랜지스터의 수가 늘어날수록 더 복잡한 연산이 가능해지고 우리가 사용하는 디지털 기계들의 가격이 크게 줄어든다. 그래서 우리는 이 기술을 더욱 발전시키기 위해 노력 중이다.
일단 첫번째로 논리 회로란 디지털 시스템에서 정보 처리를 위해 사용되는 회로이다. 입력 신호를 받아 만들어진 회로대로 논리 연산을 진행하고 그에 따른 출력 신호를 내보낸다. 컴퓨터 논리를 배울 때 가장 먼저 생각나는 True & False, 1과 0 이 여기서 사용된다.
오늘날의 디지털 시스템은 두 개의 binary digit (비트bit 라고도 불린다) 을 사용한다. (2진법)
여기서 0 은 거짓 (false) 를 의미하고 1은 진실/참 (true) 을 의미한다.
0 은 일반적으로 0V ~ 1V 사이이고, 1 은 3V ~ 5V 사이 정도이다.

기본적으로 논리 회로는 논리 게이트라는 연산 요소로 구성이 되는데, 가장 기본적인 게이트로는 AND, OR, NOT 이 있다.
(이후 게이트들에 대해 더 자세히 작성할 예정이라 지금은 넘어가도 괜찮은 부분입니다!)
- AND: AND 게이트는 입력이 모두 참일 때 (true) 만 출력이 되는 참이다.
- OR: OR 게이트는 입력 중에 하나 이상이 참일 경우 참을 출력한다.
- NOT: NOT 게이트는 입력을 반전 (참 -> 거짓, 거짓 -> 참) 시켜 출력한다.
또한 이런 기본 게이트들을 조합해 만들어낸 게이트로 NAND, NOR 이 있다.
- NAND: AND의 출력을 반전시킨다. 입력이 모두 참일 때 거짓을 출력한다.
- NOR: OR의 출력을 반전시킨다. 입력 중 하나 이상이 참일 때 거짓을 출력한다.
이러한 게이트들을 연결하여 회로로 만들어낸 것이 논리 회로인데, 여기서 중요한 것은 효율적인 회로를 만들어 내는 것이다.
Chapter 1. r진수와 진수의 변환
디지털 논리 회로에는 진수가 정말 큰 부분을 차지한다. 그러므로 수를 여러 진수로 바꾸는 법을 아는 것이 중요하다.
먼저 우리가 일상 생활에서 가장 많이 사용하는 진법은 10진법이다 (r=10). 0~9 까지를 사용해 1의자리, 10의자리, n의 자리에 넣어 표현한다.
예시) 7392 (10) *괄호 안의 10은 10진수라는 것을 뜻한다. 지수의 밑 = 10
1의 자리 수: 2
10의 자리 수: 9
100의 자리 수: 3
1000의 자리 수: 7
이것을 더해 칠천삼백구십이 가 되는 것이다.
식: (1x2) + (10x9) + (100x3) + (1000x7) = 7392
그리고 2진수(r=2) 는 0과 1 로만 이루어진 숫자를 이진수라 부른다.
예시) 11010.11 (2)
r진수 --> 10진수
r진수들을 10진수로 변환시키려면 아래의 공식을 사용하면 쉽다.

위의 수학 공식들이 익숙하지 않으신 분들이 있으실 수 있으니 간단하게 풀어 설명하자면,
∑ 기호는 (sum) 더해 주어야 한다는 의미이다. 이 기호와 위에 있는 (n-1), 아래의 (i=0) 는 변환하고 싶은 r진수의 모든 자릿수의 숫자를 더해 준다는 의미이다.
그리고 조건 (0 ≤ ai < r) 은 r진수를 이루고 있는 숫자가 r 보다 크거나 같을 수 없고, 0 이상이어야 한다는 의미이다.
우리가 잘 아는 10진수를 보면 이루고 있는 각각의 자릿수 숫자들이 10을 넘어가지 않는 것을 알 수 있다 (전부 0~9 사이).
그렇다면 이제 이 공식에 대입을 해 보자.

이진수 101.01 (2) 를 10진수로 변환하면 5.25 가 되는 것을 알 수 있다. 사실 2진수에서 "0" digit 들은 전부 곱해주면 0이 되므로 일일이 적을 필요 없이 무시해주면 된다.
아래는 각각 5진수와 8진수의 변환 예시이다.

그리고 10진수 이상 (r > 10) 의 진수들은 조금 다르게 표현하는데, 그중 많이 쓰일 16진수는 숫자 0부터 9, 그리고 문자 A 부터 F 까지를 사용해 나타낸다. (A ~ F 는 10부터 15 를 나타낼 때 사용)

위의 예시대로 16진수인 B65F (16) 을 10진수로 변환해주면 46687 (10) 이라는 것을 알 수 있다.
십진수 --> r진수
이렇게 r진수를 십진수로 변환해 보았는데, 그 반대 경우의 십진수에서의 r진수 변환을 보자.

변환하는 방법은 간단하다.
1) 변환하고 싶은 10진수를 r 로 나눈다
2) 정수인 나머지가 계수가 된다
3) 정수인 몫이 다음으로 나누어질 숫자가 된다
4) 몫이 0이 될 때까지 반복 (정수 부분의 몫이 0이 될 때까지)

이렇게 표를 그리면 더욱 보기 쉽게 변환 할 수 있다.
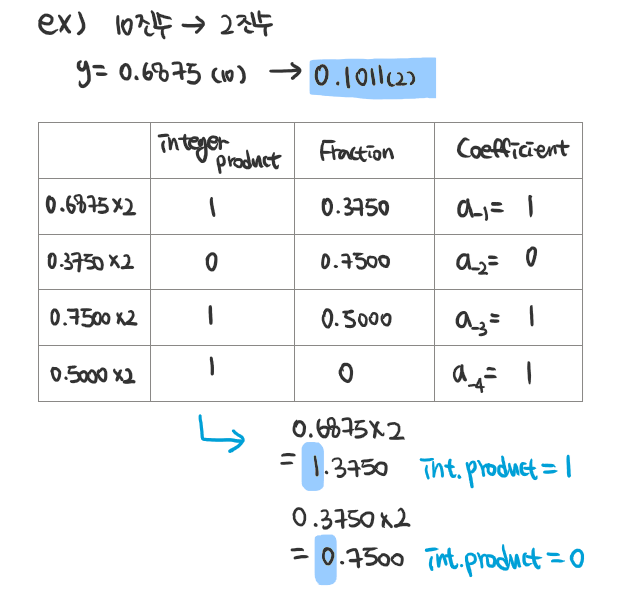
소수점 자리의 변환법
소수점 자리는 방법이 조금 다르다.

1) 10^-1 자릿수부터 시작한다
2) 숫자를 r 의 값으로 곱해준다
3) 곱해서 나온 값의 정수 부분이 계수가 된다
4) 소수점 자리 부분은 다음에 곱해준 숫자가 된다
5) 0이 될 때 가지 반복한다 (소수점 자리 부분이 0이 될때까지)
그리고 중요한 것은: 만약 소수점 자리와 정수 자리를 둘 다 포함한 경우, 둘을 각각 다른 방식으로 변환해 마지막에 더해주어야 합니다!!
예시로, 41.6875 (10) 을 2진수로 변환하면
41 (10) = 101001 (2)
0.6875 (10) = 0.1011 (2)
더해서 = 101001.1011 (2) 이 된다.
2,8,16진수끼리의 쉬운 변환법
2진수와 8진수, 그리고 16진수끼리는 서로 변환이 쉽다.
2^3 = 8, 그리고 2^4 = 16 이라는 점을 이용 할 수 있는데, 2진수를 각각 8진수로 변환 할 때는 3개씩 묶어 변환하고 16진수로 변환할 때에는 4개씩 묶어 변환을 진행하면 된다.

2진수의 음수 표현법
컴퓨터가 음수를 표현하려면 조금 특별한 방식을 사용해야 한다. 컴퓨터는 뺄셈을 하기 힘들어 하기 때문에, 덧셈을 이용해야 하는데 이걸 위해 보수(complement of numbers) 가 만들어졌다.
보수의 개념은 우리가 생각하는 음수와는 많이 다른데, "보수" 라는 말 그대로 어떠한 수를 보충해주는 수라 생각하면 쉽다. (예를 들어 10에 대한 50의 보수를 알아보자.
10이 50이 되려면 40이 필요하다. 하지만 우리가 말하는 "n의 보수"는 n의 제곱수가 되게 하는데 필요한 수를 말한다.
그러니 가지고 있는 숫자 10 이 50의 제곱인 2500이 되려고 할 때 필요한 수를 찾아야 한다.
10 이 2500이 되려면 2400을 더해주면 된다. 따라서 10에 대한 50의 보수는 2400인 것이다.)
보수는 두 가지 종류가 있는데, (r-1)의 보수 ((r-1)'s complement) 와 r의 보수 (r's complement) 가 있다.

*왼쪽의 영어 필기 부분을 오른쪽 한국어로 번역한 것입니다
각각의 보수를 알아보자.
첫번쨰로, (r-1) 의 보수 (Diminished Radix Complement) 는 정수부분 n자릿수와 소수점 부분 m자릿수로 이루어진 r진수가 있을 때 N에 대한 보수식은 아래와 같다:

만약 소수점 뒤의 자리수가 있다면, 공식에서 m 자리에 소수점 아래의 수만큼 넣어 계산하면 된다.
쉽게 하는 법: 예시를 보고 알아차린 분들이 많으실 것 같은데, 별다른 소수점의 자리가 없을 경우 정수부분의 자릿수 n 만큼 원하는 보수 (r-1) 의 값을 적어 주어진 N 을 빼 주면 된다.

위의 예시는 10진수를 이용하였지만, 이제는 2진수를 사용해 보수를 찾아보자.

역시 방법은 같은데, 공식에 각 주어진 자릿수와 r진법만큼 대입시켜 계산하면 된다. 하지만 2진법의 경우 더욱 쉽게 하는 법이 있는데, 그건 바로 비트를 뒤집어 주면 된다. 아무런 계산이 필요하지 않다.

*2진수의 뺄셈 계산법을 설명하지 않았다는 것을 방금 알아차렸어요! 다음 편에 2진수의 덧셈 뺄셈에 대해 적겠습니다*
하지만 주의해야 할 점이 있는데, 만약 자릿수가 따로 주어진 경우, 그 값은 매우 달라 질 수 있으니 조심해야 한다.
예시로 0546700이라는 수가 있을 때, 우리가 흔히 생각하는 방법으로 보면 맨 앞자리의 0은 유효하지 않으니 떼어버리고 546700으로 무심코 읽을 수 있는데, 앞자리의 0 또한 자릿수로 생각하고 계산을 해 주어야 한다. 그러므로 주어진 자연수의 자릿수를 6이 아닌 7으로 두고 계산하여야 한다는 것이다.

이제 r의 보수 (Radix Complement) 를 알아보자.

그대로 공식에 주어진 자릿수와 수, 그리고 r진법의 r을 대입하면 계산 할 수 있다.
하지만 더욱 쉽게 하는 법이 있는데, 그건 바로 (r-1)의 보수를 구한 후 거기서 +1을 해 주면 r의 보수가 된다.

위의 (r-1)의 보수에서 설명했듯 2진수에서 1의 보수를 구하려면 비트를 전부 뒤집으면 된다. 그 후, +1을 해주면 바로 2진수의 2의 보수를 구할 수 있다.
10진수도 마찬가지인데, 주어진 수의 9의 보수를 구한 후 단순히 +1을 해 주면 10의 보수를 구할 수 있다.
Summary
- 0: false (0V~1V), 1: true (3V~5V)
- 진수 변환에서 소수점 자리와 정수 자리를 둘 다 포함한 경우, 각각을 따로 변환해 더해주어야 한다
- 2진수와 8진수, 그리고 16진수끼리는 서로 변환이 쉬운데, 2진수를 각각 8진수로 변환 할 때는 3개씩 묶어 변환하고 16진수로 변환할 때에는 4개씩 묶어 변환을 진행하면 된다.
- 2진법의 (r-1)의 보수 (1의 보수) 는 모든 비트를 뒤집어주면 된다 (0 <--> 1)
- r의 보수는 (r-1)의 보수를 구한 후 +1을 해 주면 된다
이렇게 r진수 변환에 대해 알아보았는데, 사실 다른 진수들이 익숙하지 않아 처음에는 헷갈리지만 많이 접해서 연습을 하면 이후 연산 부분을 편하게 할 수 있으므로 잘 알아두는 것이 좋습니다.
다음 글은 r진수와 그 연산방법을 소개하고 있습니다! (2진수의 연산도 포함)
+ 처음에 혹시 제 글씨를 알아보지 못하실까봐 공식을 타이핑 했었는데, 역시 수학 공식 타이핑은 시간이 오래 걸리네요ㅠㅠ 이렇게 캡쳐해서 첨부하는 방식으로 하겠습니다!


