* 틀린 내용이 있다면 알려주세요! 개인 공부 목적으로 전공 복습/예습을 위해 쓰는 글이라 틀린 부분이 있을 수 있습니다. 틀린 내용을 알려주시면 제게도 도움이 됩니다 :)
* 해외 대학을 재학 중이기 때문에 영어 사용이 조금 많을 수 있지만 최대한 한국어로 번역하려 노력중입니다.
* 효율적인 타이핑을 위해 "~이다" 의 문체를 사용합니다. 양해 부탁드립니다!
지난 글에서 소개했던 부울대수 기초를 이어서 작성했습니다. 혹시 이전 글을 읽지 않으셨다면 헷갈릴 수 있으니 읽고 오시는 걸 추천드립니다!
https://wlqdprkffo.tistory.com/4
[2] DLD I (디지털 논리 설계): 부울대수, Boolean Algebra
* 틀린 내용이 있다면 알려주세요! 개인 공부 목적으로 전공 복습/예습을 위해 쓰는 글이라 틀린 부분이 있을 수 있습니다. 틀린 내용을 알려주시면 제게도 도움이 됩니다 :) * 해외 대학을 재학
wlqdprkffo.tistory.com
Chapter 2: 부울대수 Boolean Algebra
최소항 (minterms) 과 최대항 (maxterms)
부울함수의 진리표를 만들어 보면 최소항(minterms) 과 최대항(maxterms) 를 구할 수 있는데, 이것을 이용하여 2개의 식을 각각 얻을 수 있다. 이 식을 사용해 간단한 회로를 만들 수 있는데, 이 회로는 AND 와 OR 으로 구성되어 있다.
*모든 부울 함수는 최대항, 최소항으로 표현 가능하다
먼저 최소항에 대해 설명하자면 아래의 특징을 가지고 있다.

예시에 보이는 대로 곱들의 합 형태를 가지고 있다. (AND 게이트)
그리고 최대항은 아래의 특징을 가지고 있다.

합들의 곱의 형태를 하고 있는 것을 알 수 있다. (OR 게이트)
*단, 항마다 모든 변수가 한번씩 꼭나타나야 한다.
예를들어 x,y,z 가 있을 때 (xy + x'y + zy) 란 식이 있다고 하면, 이 식은 최대항도 최소항도 아니다. 각각의 항에 모든 세 개의 변수가 다 나타나지 않았기 때문이다.
최소항과 최대항의 예시를 보자.

식 F = xy + x'z 에 대한 진리표를 만들면 위와 같다. 여기서 결과값 F =1인 것은 최소항이고 (초록색), F=0 인 것은 최대항이다 (분홍색).
최소항을 먼저 보면, 각각 1,3,6,7 자리에 해당하는 값들이 F=1 인 것을 알수 있다 (진리표 F 줄 옆의 작은 파란색 순서번호). 그래서 F(x,y,z) = ∑ (1,3,6,7) 혹은 m1+m3+m6+m7 으로 표현할 수 있다.
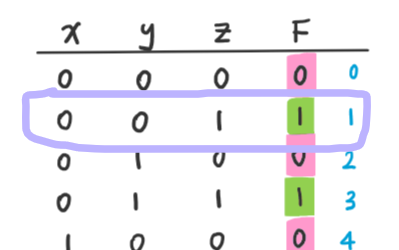
이 최소항들을 식으로 표현할 때, 먼저 m1: x=0, y=0, z=1 인 것을 위의 표에서 확인 할 수 있다 (보라색으로 표시된 곳이 m1 에 해당한다). 최소항은 앞서 말했듯이 곱의 합이므로 모두 나타내면 m1+m3+m6+m7 = 001 + 011 + 110 +111 이 된다.

여기서 0 = x', y', z' 이고 1 = x, y, z 이라고 하면, F = x'y'z + x'yz + xyz' + xyz 라는 식이 완성된다.
이것을 부울대수의 법칙을 이용해 단순화시키면 최종적으로 최소항은 x'z + xy 의 식으로 표현될 수 있다.
간단화 시키는 과정을 잠깐 설명하자면,
1. 공통으로 가진 항이 있는지 확인한다. 예시에선 각각 2 개의 항들이 x'z, 그리고 xy 를 포함하고 있다.
2. x'z 를 가진 두 항들을 서로 묶어주고 x'z 를 괄호 바깥으로 빼내 준다 (분배법칙)
3. xy 를 포함한 항들도 같은 방법으로 묶어준다.
4. x'z, xy 를 뺀 후 남은 괄호 안의 식이 간단화 될 수 있는지 확인한다.
5. (y'+y) 그리고 (z'+z) 는 1 이 되는 부울대수 연산 법칙대로 줄여주면 간단화된 식이 나온다.
최대항은 각각 0,2,4,5 의 자리에 해당하는 값이 F=0 이므로 F(x,y,z) = ∏ (0,2,4,5) 혹은 M0·M2·M4·M5 으로 나타낼 수 있다 (진리표 F 부분에서 분홍색으로 칠해진 곳).
최대항은 합의 곱이라는 사실을 생각하며 진리표대로 식을 만들면 F = (x'+y'+z')(x'+y+z')(z+y'+z')(x+y'+z) 이 되는데, 부울대수의 법칙들을 이용하면 xz'+x'y' 로 간단하게 만들 수 있다.

1. 공통으로 가진 항이 있는지 확인한다. 위의 예시에서는 생략되었지만 첫번째와 둘째 괄호안에 각각 x'+z' 을 공통으로 가지고 있다.
2. 분배 법칙으로 (x'+z')를 뺴내 준 후, 남은 (y'+y) 는 부울대수 연산 법칙으로 1 이 되므로 결국 (x'+z') 로 줄여진다.
3. 셋째, 넷째 괄호도 같은 방법으로 (x+y') 를 밖으로 빼 준후 (z'+z) = 1 으로 줄인다.
4. (x'+z')(x+y') 는 분배 법칙으로 괄호를 풀어준다.
5. 그 후 간단화 되는 식을 찾아준다. xx'=0
6. 그리고 부울대수 법칙 (파란색으로 써진 식)으로 최종적으로 줄여준다. 이 부분이 조금 헷갈릴 수 있을 것 같아 아래에 증명을 넣었다. 간단히 설명하자면 마지막 항 yz 에 (x+x') 을 계산하기 편하도록 추가해 준 후 (어차피 x+x'=1 이므로 값을 바꾸지 않는다) 분배해 간략화 시키는 것과 같다.

여기서 최소항과 최대항의 관계를 확인 할 수 있는데, 최소항에 없는 항들은 최대항에서 발견된다는 것을 알수 있다.
이 이유는 최소항을 이용하여 부울함수를 구하는 것과 최대항을 이용하여 부울함수를 구하는 과정은 서로 정확히 반대하기 때문이다.
다르게 말하면, 드모건 공식(DeMorgan's Theorem) 을 사용해 서로 구해진 식의 역수를 찾으면 서로 같아지는 것을 알 수 있다.
*만약 드모건 공식이 헷갈리신다면 이 글의 제일 위에 걸어둔 부울대수 1 링크에 내용이 정리되어 있습니다!
아래의 식을 보면, 위에서 구했던 최소항 m1+m3+m6+m7 = x'y'z + x'yz + xyz' + xyz 에 드모건 공식을 사용했다. 그후 간략화 시킨다면 최대항의 결과값과 같아진다는 것을 알 수 있다.

그러므로, 최소항과 최대항은 m'j = Mj 라는 관계로 정리할 수 있다.
(최소항의 역수) = 최대항
이렇게 최대항과 최소항에 대해 알아보았는데, 이를 이용해 식을 간단화 시키면 AND 와 OR로 이루어진 회로를 만들 수 있다.
Summary
- 최소항 (minterms) 은 곱의 합의 형태. 진리표에서 1의 값을 가지는 항들을 말한다.
- 최대항 (maxterms) 는 합의 곱의 형태. 진리표에서 0의 값을 가지는 항들이다.
- 드모건 공식을 사용하면 최소항과 최대항은 m'j = Mj 라는 관계로 정리할 수 있다. (최소항의 역수 = 최대항)
설명을 열심히 하긴 했는데 헷갈리지는 않을지 걱정이네요.. 나중에 다시 읽어보고 수정할 부분이 있다면 더 쉽게 풀어 설명하도록 하겠습니다!


